Bài viết này là tài liệu thi giữa kỳ trí tuệ nhân tạo cho các bạn sinh viên. Nội dung được tóm tắt ngắn gọn và minh họa các giải thuật chi tiết.
Tài liệu thi giữa kỳ trí tuệ nhân tạo
Hàm heuristic là gì ?
Heuristic là hàm ước lượng về khả năng dẫn đến lời giải. Ký hiệu là h
1. Tìm kiếm rộng (Breadth-first search) BFS
Tìm kiếm rộng dùng cơ chế FIFO (First in First out) - QUEUE – Vào trước Ra trước.
Thực hiện thuật toán BFS
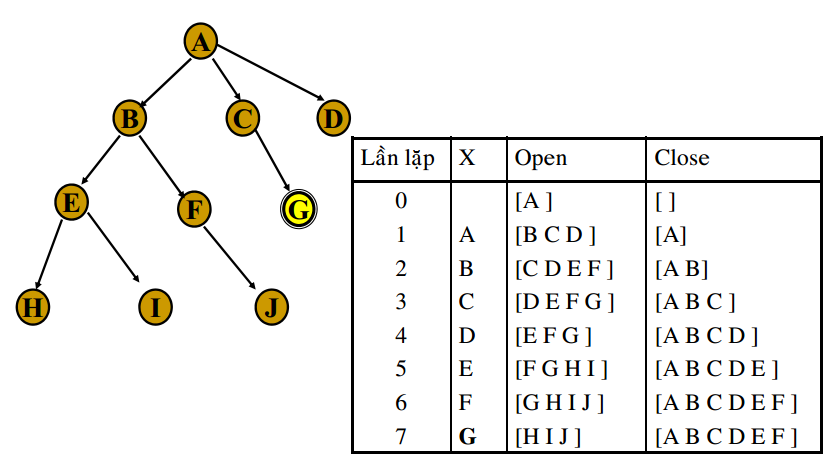
2. Tìm kiếm sâu (Depth-first search) DFS
LIFO(Last in first out) – STACK – Vào sau ra trước
Depth first search có khả năng lặp vô tận vì sao?
-> Do các trạng thái con sinh ra liên tục. Độ sâu tăng vô tận. Khắc phục bằng cách giới hạn độ sâu của giải thuật.
Thực hiện thuật toán DFS
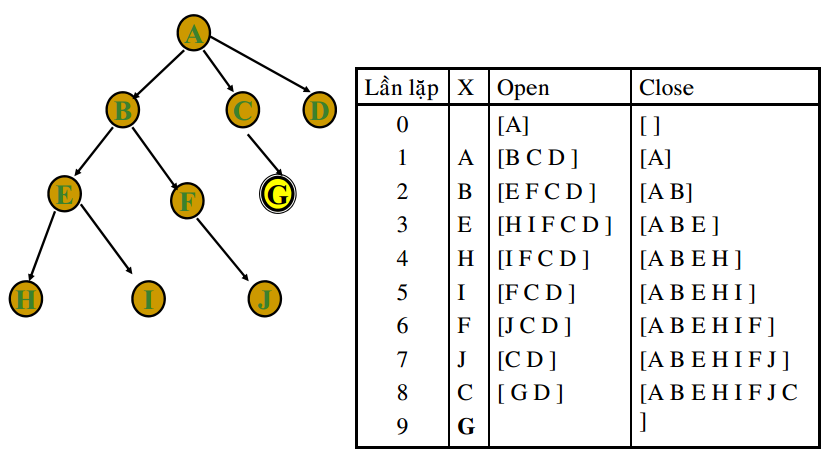
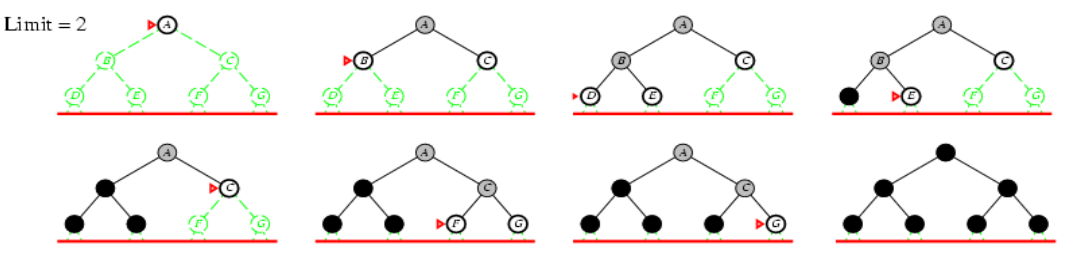
3. Tìm kiếm sâu dần (Iterative deepening search) IDS
Như DFS nhưng giới hạn(limit) độ sâu
Ví dụ:
- Độ sâu limit = 0

- Độ sâu limit = 1
 3. Độ sâu limit = 2
3. Độ sâu limit = 2
##
- Tìm kiếm leo đồi
Tìm kiếm leo đồi là một trường hợp đặc biệt của tìm kiếm theo chiều sâu nhưng không thể quay lui. Chọn trạng thái kế tiếp thực hiện bằng hàm Heuristic.
Khác với tìm kiếm sâu, leo đồi không lưu tất cả các con mà chỉ lưu đúng một trạng thái được chọn nếu có.
- Trạng thái tốt hơn: Leo đồi đơn giản
- Trạng thái tốt nhất: Leo đồi dốc đứng.
4.1 Leo đồi đơn giản
Leo đồi đơn giản chỉ chọn đi theo trạng thái kế tiếp đầu tiên tốt hơn trạng thái hiện hành mà nó tìm thấy.
Trình bày các bước của thuật giải leo đồi đơn giản.
Bước 1: Nếu trạng thái bắt đầu (T0) là trạng thái đích: thoát và báo là đã tìm được lời giải.
Ngược lại, đặt trạng thái hiện hành (Ti) là trạng thái khởi đầu (T0)
Bước 2: Lặp lại cho đến khi đạt đến trạng thái kết thúc hoặc cho đến khi không tồn tại một trạng thái tiếp theo hợp lệ (Tk) của trạng thái hiện hành:
a) Đặt Tk là một trạng thái tiếp theo hợp lệ của trạng thái hiện hành Ti.
b) Đánh giá trạng thái Tk mới:
- Nếu là trạng thái đích thì trả về trị này và thoát.
- Nếu không phải là trạng đích nhưng tốt hơn trạng thái hiện hành thì cập nhật nó thành trạng thái hiện hành.
- Nếu nó không tốt hơn trạng thái hiện hành thì tiếp tục vòng lặp.
4.2. Leo đồi dốc đứng
Giống như leo đồi đơn giản, chỉ khác ở điểm là leo đồi dốc đứng sẽ duyệt tất cả các hướng đi có thể và chọn đi theo trạng thái tốt nhất trong số các trạng thái kế tiếp có thể có.
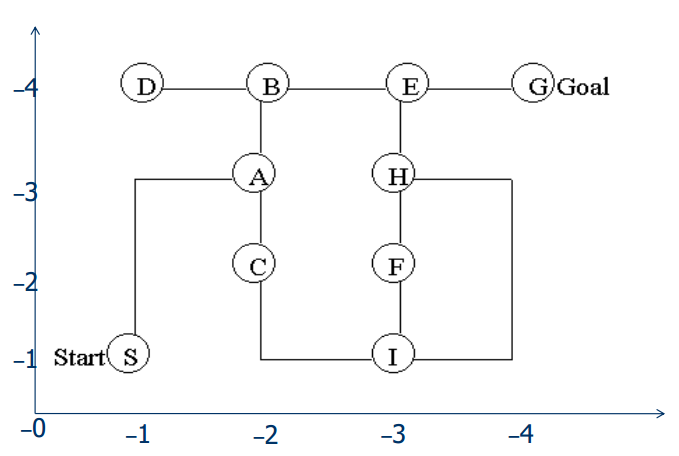
Ví dụ bài tập:
H(n) = |Tọa độ x của đích – Tọa độ x của n | + |Tọa độ y của đích – Tọa độ y của n |
n:=S
h(S)=|4-1|+|4-1|= 6 (min)
h(A)=|4-2|+|4-3|= 3 (min) < h(S)
NextS = A
n:=A
h(B)=|4-2|+|4-4|=2 (min) h(C)=|4-2|+|4-2|=4
h(B)<h(A)
NextA = B
n:=B
h(E)=|4-3|+|4-4|=1 (min) < h(B)
NextB = E
n:=E
h(G)=|4-4|+|4-4|=0 (min) h(H)=|4-3|+|4-3|=2
h(G)<h(E)
NextE = G (Đích- Dừng)
5. Thuật giải GTS (Greedy-Traveling Saleman)
5.1. GTS1
Tìm kiếm đường đi có chi phí nhỏ nhất khi qua n đỉnh với ma trận chi phí cho trước và bắt đầu tại 1 đỉnh v cho sẵn.
Bài tập:

 5.2. GTS2
5.2. GTS2
Tương tự GTS1 nhưng giải thuật này sẽ thử hết đường đi từ các đỉnh v xuất phát. Sau đó chọn ra đường đi tốt nhất.
6. Thuật toán tô màu tối ưu trên đồ thị
Thuật toán: Lặp lại các bước sau cho đến khi nào tô màu hết các đỉnh
Bước 1: Chọn đỉnh có bậc lớn nhất tô màu i.
Bước 2: Hạ bậc:
Đỉnh đã tô màu: bậc = 0
Những đỉnh có liên hệ: bậc := bậc – 1
Bước 3: Đánh dấu các đỉnh liên hệ (bậc vừa trừ đi 1) cấm tô màu i
Ví dụ: Phân công, lịch công tác, lịch thi đấu:
Có một cuộc hội thảo khoa học với 9 chủ đề khác nhau, mỗi chủ đề diễn ra trong một buổi.
Các chủ đề sau không được đồng thời: AE, BC, CD, ED, ABD, AHI, BHI, DFI, DHI, FGH.
Xây dựng lịch sao cho số buổi diễn ra là ít nhất. Gợi ý: số màu = số buổi.
=>Giải:

 Kết luận:
Kết luận:
Buổi 1: G, D; Buổi 2: C, E, H; Buổi 3: A, F; Buổi 4: B; Buổi 5: I
7. Thuật giải AT (Algorithm for Tree)
Trình bày các bước của thuật giải AT
Bước 1:
- Mọi đỉnh n, mọi giá trị g(n) đều là ẩn.
- Mở đỉnh đầu tiên và gọi đó là đỉnh S. Đặt g(S) = 0.
Bước 2: Chọn đỉnh mở với giá thành g tương ứng là nhỏ nhất và gọi đó là đỉnh N. - Nếu N là mục tiêu: đường đi từ đỉnh ban đầu đến N là đường đi ngắn nhất và bằng g(N). Dừng (Success).
- Nếu không tồn tại một đỉnh mở nào nữa: cây biểu diễn vấn đề không có đường đi tới mục tiêu. Dừng (Fail).
- Nếu tồn tại nhiều hơn 1 đỉnh N (nghĩa là có 2 đỉnh N trở lên) mà có cùng giá thành g(N) nhỏ nhất. Kiểm tra xem trong số đó có đỉnh nào là đích hay không.
Nếucó:đườngđitừđỉnhbanđầuđếnđỉnhNlàngắnnhấtvàbằngg(N),dừng(Success).
Nếukhôngcó:ChọnngẫunhiênmộttrongcácđỉnhđóvàgọilàđỉnhN.
Bước 3: Đóng đỉnh N và mở các đỉnh sau N (là những đỉnh có cung hướng từ N tới). Tại mọi đỉnh S sau N tính :
g(S)=g(N)+cost(N->S)
Bước 4: Quay lại bước 2
8. Thuật giải AKT – Tìm kiếm với tri thức bổ sung (Algorithm for Knowledgeable Tree Search)
Ví dụ:
Bài toán Tháp Hà Nội với n = 2
Gọi n là tổng số đĩa cần chuyển, m là số đĩa đã nằm đúng vị trí ở cột thứ 3, k là số đĩa nằm sai vị trí ở cột thứ 3.
Có thể thấy bạn cần chuyển các đĩa nằm sai vị trí ra khỏi cột 3 (k đĩa), sau đó chuyển các đĩa chưa đúng vị trí vào đúng vị trí của nó (n-m-k đĩa), cuối cùng chuyển k đĩa sai vị trí vào lại.
Như vậy bạn sẽ có công thức là: h = k + (n-m-k) + k = n-m+k.


9. Thuật giải A* - tìm kiếm đường đi trên đồ thị tổng quát
Trình bày các bước của thuật giải A*
Bước 1: Mọi đỉnh và
–Mọi đỉnh, cũng như các hàng g, h, f chưa biết.
–Mở đỉnh đầu tiên S, gán g(S) = 0
–Ước lượng hàm h(S)
–Gán f(S) = h(S)+ g(S)
Bước 2: Chọn đỉnh mở có f(S) là nhỏ nhất và gọi là đỉnh N
- Nếu N là đích: đường đi từ đỉnh ban đầu đến đỉnh N là ngắn nhất và và bằng
g(N).Dừng(Success). - Nếu không tồn tại đỉnh mở nào: cây biểu diễn vấn đề không tồn tại đường đi
tớimụctiêu.Dừng(Fail). - Nếu có 2 đỉnh mở trở lên có cùng giá trị f(S) nhỏ nhất: ta phải kiểm tra xem
nhữngđỉnhđócóđỉnhnàolàđíchhaykhông.
- Nếu có: đường đi từ đỉnh ban đầu đến đỉnh N là ngắn nhất và bằng g(N). Dừng (Success).
- Nếu không có: chọn ngẫu nhiên một trong các đỉnh đó và gọi đỉnh đó là N.
Bước 3:
–ĐóngđỉnhN,vàđốivớimỗiđỉnhSsauN,chúngtatính:
–g’(S)=g(N)+cost(S->N)
–NếuđỉnhSđãmởvàg(S)<=g’(S)thìbỏquaS
–NgượclạimởSvàđặtg(S)=g’(S),tínhh(S)vàf(S):f(S)=g(S)+h(S)
Bước 4: Quay lại bước 2.
Link tải đầy đủ tài liệu thi giữa kỳ trí tuệ nhân tạo: Ôn TTNT GK